|
That comment raised my hackles. How can you not care what pictures are on the wall. I gladly spend After my hackles had retracted, I realized that the director's ability to delegate had something to do with how he managed to make 26 films in the past 20 years, a number of them quite good. Over the years, I've gotten better at managing time. That's not saying much, in light of how bad I used to be at it. But really, my point is just that I love the phrasing of "you couldn't pay me enough to care about that." From the CVR transcript from USAir flight 1549:
Much has been said about how the pilots' experience and training prepared them for this emergency: how they knew what to do, how they worked together as a team, and so on. Their expertise shows in the transcript, but something more basic shows as well: they kept their cool. I grew up in a household of people who were often not so good at keeping their cool. Undoing what I learned from their example is an ongoing process, and continues to be worth the effort (even though I don't fly airplanes). I watched a movie from 1999 yesterday and it looked so dated, because all the televisions and monitors were CRTs. CRTs are not just outmoded, they are positively ponderous. I mean, not all older technology looks so clunky. Books still appeal. Which gives me a segue to offering two closeups of books as depicted on banknotes--
My manager gave awards to a couple of us before the project was finished, which I saw as a way of saying don't disappoint us by not finishing on schedule. It struck me as somewhat crafty, but I was more impressed than irked by the tactic (and I appreciated the recognition in any case). We delivered the work on time. But a tactic that's OK for a small-potatoes award is not necessarily appropriate for something as large as, say, the Nobel Peace Prize. A line from today's press release (emphasis mine) suggests that this year's prize is at least partly about influencing the future (as opposed to recognition of achievement): For 108 years, the Norwegian Nobel Committee has sought to stimulate precisely that international policy and those attitudes for which Obama is now the world's leading spokesman.But setting aside issues specific to this year's choice--a Peace Prize is inherently problematic for a bunch of reasons. As important as peace is, I think Mr. Nobel would have done well to have stuck to categories where there tends to be more consensus on the merits of nominees. From an obituary for mathematician Israel Gelfand: "Mathematics is a way of thinking in everyday life," Dr. Gelfand said in a 2003 interview with The New York Times. "It is important not to separate mathematics from life. You can explain fractions even to heavy drinkers. If you ask them, 'Which is larger, 2/3 or 3/5?' it is likely they will not know. But if you ask, 'Which is better, two bottles of vodka for three people, or three bottles of vodka for five people?' they will answer you immediately. They will say two for three, of course."What's more, people can have an intuitive sense of more difficult comparisons. For example-- Which is more rare, a palindromic eight-digit serial number, or one that consists of only two digits? And are they close (i.e. nearly equally rare) or is one a lot more common? Please comment with your guess (i.e., don't do the calculation first). By "only two digits", I mean any pair of two digits. So either of the two $1 bills pictured is such a specimen. The letters don't count.
A street has houses numbered 1 through m, consecutively. The sum of all numbers below that of a particular house (call its number n) equals the sum of all the numbers above it.The task is to find positive integers n and m such that 1 + 2 + ... + n-1 = n+1 + n+2 + ... + m. Ramanujan famously gave the general solution in the form of a continued fraction. I'll get to that in a moment, but first a solution using nothing beyond high school algebra:
So n=6, m=8 should solve the original problem. It does: 1 + 2 + 3 + 4 + 5 = 7 + 8. The third and fourth powers, and the solutions they give:
Now, to express this by means of a continued fraction. We don't know which particular continued fraction Ramanujan gave, but I'll show how to construct one that may have been his answer. √8 is somewhat less than 3. What fraction less? We'll call the difference 1/x and see what we can say about it.
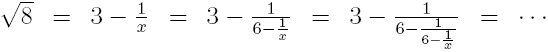
To discard the -1/x terms in these expressions is to truncate the continued fraction, which yields a sequence of ever-closer rational approximations to √8: 
these expressions simplify to:
These fractions are built from the same integers as are the powers
of (3 ± √8) as shown above. The denominators
1, 6, 35, 204, ... are house numbers n
in successive solutions to the original problem. The numerators
3, 17, 99, 577, ... are corresponding values of 2m+1.
In the interest of brevity, I haven't explained why this continued fraction for √8 does the trick. I hope, though, that this helps in appreciating the kinds of problems Ramanujan could solve intuitively. Thanks to John Butcher of The University of Auckland for his paper On Ramanujan, continued fractions and an interesting street number, where I found key elements of this solution. A copy is here in case the link is dead. Yesterday morning, around 3 A.M., I was woken up by an earthquake. It seemed to have happened in the middle of a dream that had an earthquake-y theme to it, which I thought was a cool coïncidence. I tried to recall the details of the dream so I could write them down and maybe even blog about them--but it was not to be. Memory of the dream slipped from my grasp, lost for good. I don't even know if whatever seemed earthquake-y about the dream was made up after the fact of the earthquake. I suspect that dream episodes can be constructed in a flash, and that one's sense of present time is diffuse and unreliable during and while coming out of dreams. So all I have now is a vague memory of thinking I had a dream that might not even have been a cool coïncidence: thin gruel for subject matter, which I wouldn't bother writing about except that yesterday's earthquake sets the context for... Today. I was treated to three decent earthquakes in quick succession around sundown. I was struck by how a matter of quantity evoked a difference in quality. That is, the first two earthquakes today were entertaining but the third (and several littler ones that followed) started to feel ominous. There, we just had another (i.e., after I wrote the last sentence but before I wrote this one). English uses the suffix -ing to turn a verb into a noun. German has several verbal noun forms, some of which add a connotation of there's-more-of-this-going-on-than-I'd-like. That's the line that got crossed with earthquake #3 this evening. That's not to say I'm really annoyed. I have mixed feelings. The earthquake that came in the middle of writing this entry was partly entertaining and partly unsettling. None of these quakes was strong enough to break anything. Truth is, the odds are good that my roof won't collapse on me overnight. |
